Interior Angles of a Polygon Formula

By Oto_585Emilio 03 Sep, 2022 Post a Comment

The sum of all the interior angles of any pentagon is always equal to 540. The formula is where is the sum of the interior angles of the polygon and equals the number of sides in the polygon.

Image Result For Polygon Interior Angles Regular Polygon Math Charts Polygon

Euclidean geometry is assumed throughout.

. Find the fifth interior angle of a pentagon if four of its interior angles are 108 120 143 and 97. Interior Angles The Interior Angle and Exterior Angle are measured from the same line. A pentagon has 5 sides and can be made from three triangles so you know what.

It helps us in finding the total sum of all the angles of a polygon whether it is a regular polygon or an irregular polygon. Set up an equation by adding all the interior angles presented. The number of sides of a pentagon is n 5.

The formula to calculate each interior angle of a regular Polygon. Examples Using Formula for Finding Angles. Interior angle The sum of the interior angles of a simple n-gon is n 2 π radians or n 2 180 degreesThis is because any simple n-gon having n sides can be considered to be made up of n 2.

A polygon with at least one interior angle is greater than 180 is called a non-convex polygon or concave polygon. An Interior Angle is an angle inside a shape. The diagonals of the convex polygon lie completely inside the polygon.

The formula for calculating the size of an interior angle in a regular polygon is. S n 2 180 This is the angle sum of interior angles of a polygon. All 45-45-90 triangles are similar because they all have the same interior angles.

A polygon is a two dimensional closed and flat with multiple corners. The formula to find the sum of interior angles of a regular Polygon when the value of n is given. Interior angle - n - 2180n.

All the Exterior Angles of a polygon add up to 360 so. The interior angles of a polygon are angles inside the shape. The other part of the formula is a way to determine how many triangles the polygon can be divided into.

Set up the formula for finding the sum of the interior angles. Traverse through this huge assortment of transversal worksheets to acquaint 7th grade 8th grade and high school students with the properties of several angle pairs like the alternate angles corresponding angles same-side angles etc formed when a. Each corner has several angles.

This level helps strengthen skills as the number of sides ranges between 3 25. If the polygon is regular we can calculate the measure of one of its interior angles by dividing the total sum by the number of sides of the polygon. Its interior angles add up to 3 180 540 And when it is regular all angles the same then each angle is 540 5 108 Exercise.

The two most important ones are. By using this formula we can verify the angle sum property as. Exterior Angles Sum of Polygons.

Determine the sum of the interior angles using the formula. The exterior angles of a polygon are angles outside of the shape formed between any side of the polygon and a line extended from the side next to it. Each exterior angle must be 360n.

Also a regular pentagon has all its interior angles with the same measure. The sum of the exterior angles of a polygon is 360. Since the interior angles of a regular pentagon are equal we have to divide 540 by 5 to find the measure of each interior angle.

Interior angles of a polygon. The interior angle of a convex polygon is strictly less than 180. We can use the same formula but re-worked for Radius or for Side.

A triangle is a form of a polygon with three sides or edges and vertices. An exterior angle of a polygon is made by extending only one of its sides in the outward direction. The sum of three angles forms the interior angles in this shape which is 180 degree.

The two side lengths are congruent and their opposite angles are congruent. Where s is the length of any side n is the number of sides sin is the sine function calculated in degrees. Ideally A B and C are used to denote three sides.

Make sure each triangle here adds up to 180 and check that the pentagons interior angles. The sum of the interior angles of a polygon of n sides can be calculated with the formula 180n-2. Formulas of Regular Polygon.

Hence we can say now if a convex polygon has n sides then the sum of its interior angle is given by the following formula. The value 180 comes from how many degrees are in a triangle. The sum of interior angles div number of sides.

Relationship of interiorexterior angles. What is the Sum of the Interior Angles of a Polygon. If you know the length of one of the sides the radius is given by the formula.

The formula is derived considering that we can divide any polygon into triangles. Any polygon has as many corners as it has sides. Sides of a triangle form the basic shape in geometry.

The sum of interior angles of any polygon can be calculated using a formula. The sum of an interior angle n-2 x 180⁰. The sum of all 5 interior angles of a pentagon 180 n -2 180 5 -.

Sum of all the interior angles of a polygon of n sides n 2180. Where n is the number of sides of the Polygon. Substitute the number of sides of the polygonsn in the formula n - 2 180 to compute the sum of the interior angles of the polygon.

The hypotenuse longest side is the length of either leg times square root sqrt of two 2. The polygon is an isosceles right triangle.

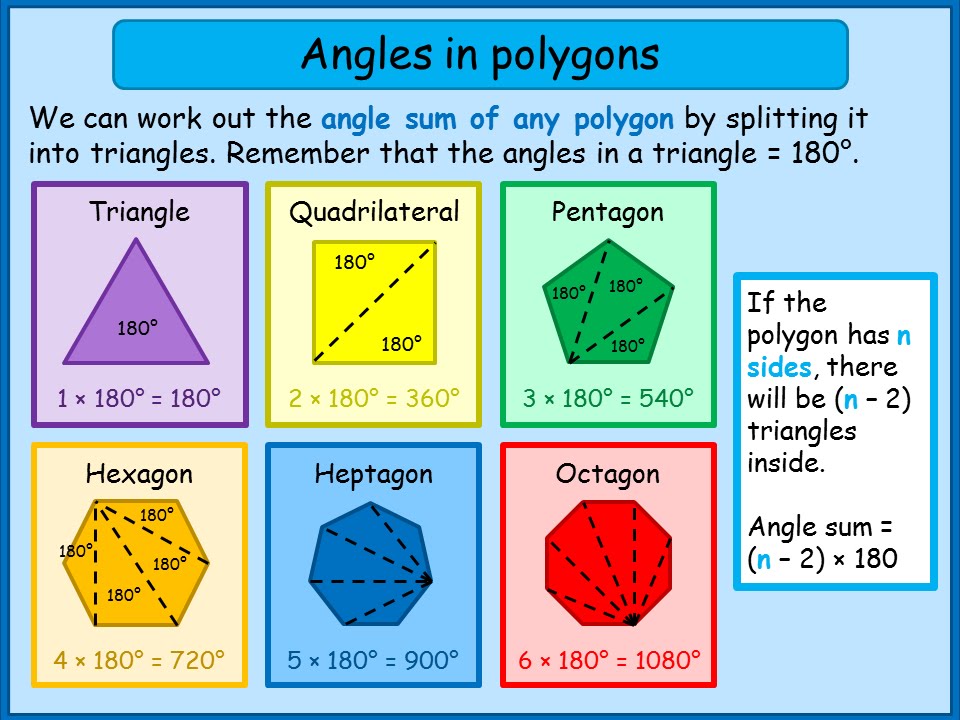
11 Angle Sum Of Any Polygon Maths Tutorials Youtube Math Tutorials Math For Kids Math Activities